题解 P1268 树的重量

发表于 | 更新于

题意:给出一个树的叶子节点间的距离，求树的边权和

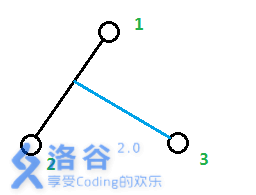
由于所有点均为叶子节点，很显然点$3$是从点$1$到点$2$的路径上分叉出来的

设蓝色部分长度为$len$，那么答案就是$g(1,2)+len$。$len$怎么求呢？显然，$len =\frac{g(1,3)+g(2,3)-g(1,2)}{2}$。

$n>3$的情况也同理。枚举$i$，看看点$n$是不是从点$1$~$i$的路径上分叉出来的，求出的最小$len$就是要加到答案里面去的。

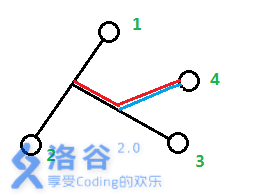
如果认为点$4$是从$1$~$2$的路径上分叉出来的，答案就会加上红色部分的长度。但是红色部分长度显然有一部分是多余的。只有认为点$4$是从$1$~$3$的路径上分叉出来的，才能加上正确答案（也就是蓝色部分）。所以对于当前点我们要枚举是从那一条路径中分叉出来的，取最小值。

证明：因为在最小的情况下，不会有任何冲突的地方，这样加点，可以保证时时刻刻没有冲突，而没有冲突的情况下答案是唯一的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
#define ll long long
#define sqr(x) ((x)*(x))
using namespace std;
inline void write(int x) {if (x<0) putchar('-'),x=-x;if (x>=10) write(x/10);putchar(x%10|'0');}
inline void wln(int x) {write(x);puts("");}
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
int a[3000][3000],ans;
int main(){
    while (1){
        int n=read();
        if (!n)return 0;
        for (int i=1;i<=n;++i)
            for (int j=i+1;j<=n;++j)
                a[i][j]=a[j][i]=read();
        ans=a[1][2];
        for (int i=3;i<=n;++i){
            int mn=2100000000;
            for (int j=2;j<i;++j){
                mn=min(mn,(a[1][i]+a[i][j]-a[1][j])/2);
            }
            ans+=mn;
        }
        printf("%d\n",ans);
    }
    return 0;
}